深度网络连接范式演进:残差连接 → 超连接 (HC) → 流形约束超连接 (mHC)
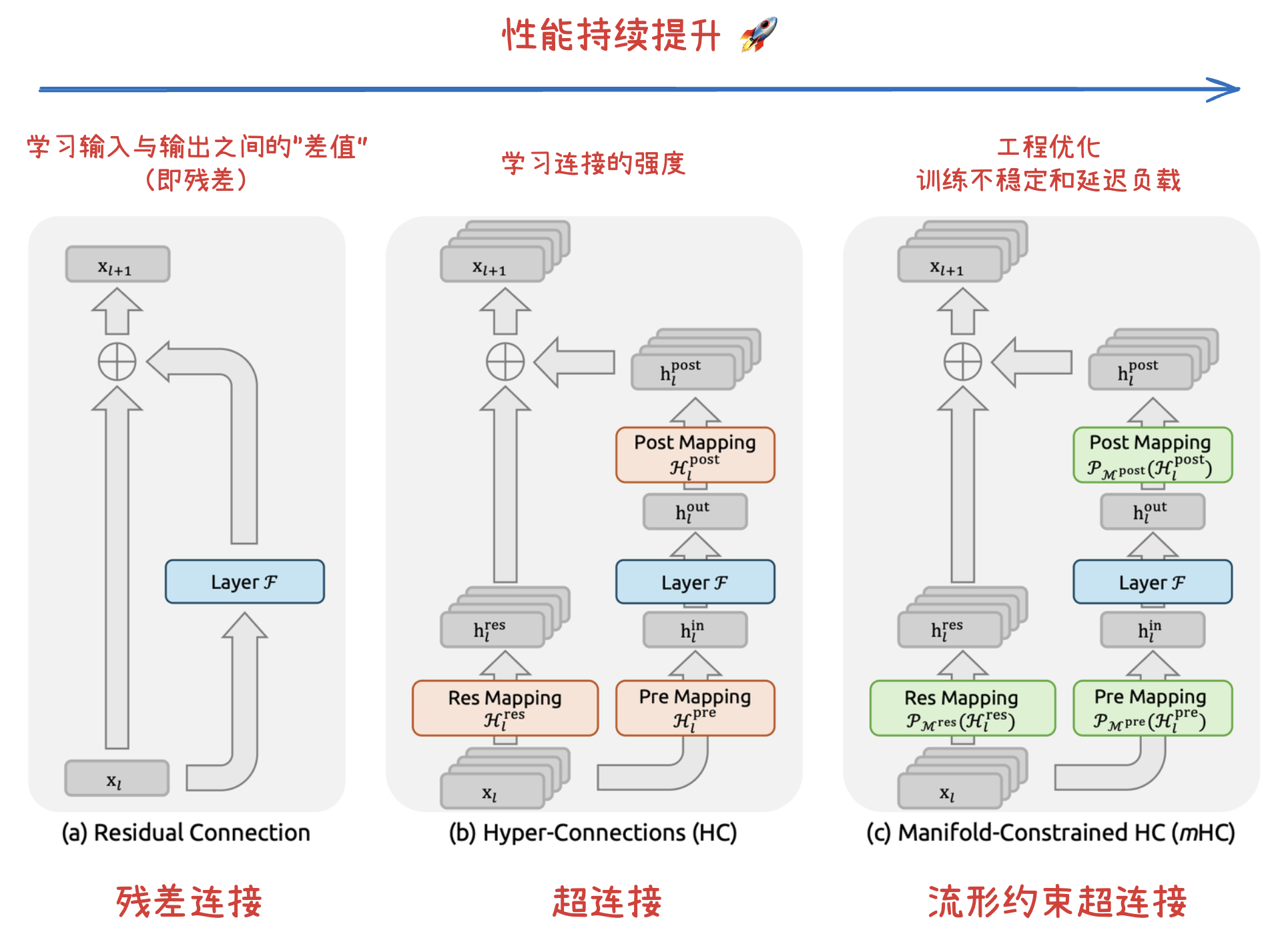
深度神经网络架构的演进,本质上是在寻找梯度稳定性与特征表达力的最优解:残差连接 通过恒等映射初步破解了深层网络的退化难题,但在缓解梯度消失与防止表征坍缩之间仍存在“跷跷板效应”;超连接(HC) 在此基础上打破了固定连接的束缚,通过引入可学习的深度连接与宽度连接,允许网络“自主学习最优连接强度”,显著提升了大模型训练的性能;流形约束超连接(mHC) 则通过将 HC 的连接矩阵投影至双随机流形,利用数学上的凸组合约束恢复了恒等映射的数值稳定性,并辅以算子融合、选择性重算和 DualPipe 通信重叠等工程优化,最终在大模型训练中实现了训练稳定性和显著降低延迟负载。
深度神经网络
梯度消失与梯度爆炸
在深度学习中,梯度消失(Vanishing Gradient) 和 梯度爆炸(Exploding Gradient) 是训练深层神经网络时经常遇到的两个核心障碍。
它们本质上是由于神经网络在反向传播过程中,梯度通过多层链式法则累积相乘导致的数值稳定性问题。
数学根源:链式法则的连乘效应
在反向传播时,我们需要计算损失函数对某一层权重的偏导数。根据链式法则,对于每一层,其梯度贡献项通常与激活函数的导数以及权重的数值有关。
- 梯度消失: 如果每一层的梯度项都小于 1(例如使用 Sigmoid 激活函数,其导数最大值仅为 0.25),经过 层连乘后,梯度会呈指数级衰减。当层数很多时,靠近输入层的梯度会变得接近于 0,导致权重无法更新,网络停止学习。
- 梯度爆炸: 如果每一层的权重较大(例如 ),且激活函数的导数也大于 1,梯度会随着层数的增加呈指数级增长。这会导致权重更新步长过大,数值溢出(出现
NaN),模型剧烈震荡甚至崩溃。
它们的影响
| 现象 | 表现 | 后果 |
|---|---|---|
| 梯度消失 | 训练损失(Loss)下降极其缓慢,或者停留在某个值不再变化。 | 浅层网络学不到特征,深度失去了意义。 |
| 梯度爆炸 | 损失函数波动剧烈,或者直接变为 NaN。 |
权重变得无穷大,模型无法收敛。 |
解决方法
归一化技术(Normalization)
- 批量归一化 (Batch Normalization): 在每一层之后对数据进行归一化处理,使其分布保持在激活函数的非饱和区,控制了梯度的数值范围。
权重初始化策略
- 初始化:通过精心设计的数学方法初始化权重的方差,使得信号在每一层传递时既不会由于过大而爆炸,也不会由于过小而消失。
饱和与退化问题
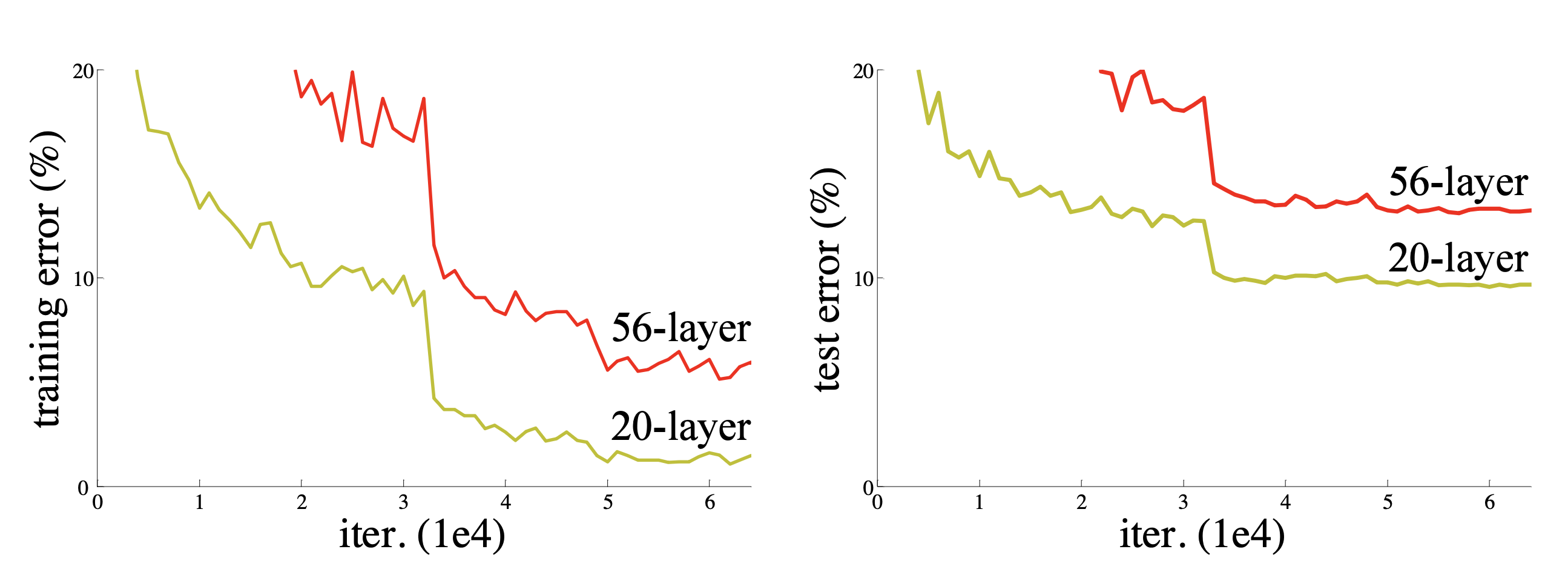
CIFAR-10 数据集上 20 层和 56 层“普通”(plain)网络的训练误差(左图)和测试误差(右图)。更深的网络具有更高的训练误差,从而也具有更高的测试误差。
饱和问题(Saturation):
随着网络层数增加到一定深度(如20层左右),继续增加层数后,测试准确率基本不再提升,甚至可能小幅波动,但整体进入一个平台期。这在深层网络中很常见,通常表明模型的容量已经足以处理当前任务,进一步加深带来的收益递减。
退化问题(Degradation Problem):
当网络深度进一步增加(如从20层增加到56层)时,不仅测试准确率停滞,甚至训练准确率也会显著下降。这意味着模型连训练数据都无法很好拟合,性能反而变差了。这不是过拟合问题(过拟合时训练准确率仍很高),而是更深层的优化困难,表明单纯堆叠层数会导致学习能力退化。
残差学习
概述
残差学习(Residual Learning) 是一种旨在解决深层神经网络训练难题的学习框架,由何恺明等人在2015年的论文中正式提出。它的核心思想是改变网络层学习的目标:不再让层去直接拟合一个完整的理想映射,而是去学习输入与输出之间的“差值”(即残差)。
解决的核心问题:退化问题(Degradation Problem)
在深度学习中,随着网络层数的增加,按理说模型的性能应该提升。然而,研究发现当网络达到一定深度后,准确率会达到饱和并迅速下降 。
-
并非过拟合引起:这种性能下降(退化)并不是由过拟合导致的,因为在实验中,层数更多的“普通网络”(Plain Network)不仅测试误差高,连训练误差也比浅层网络高 。
-
优化困难:这表明更深的网络难以被现有的优化算法(如SGD)有效训练 。
核心原理:残差框架
为了解决退化问题,作者提出了残差学习框架:
-
概念转换:不再让堆叠的层直接拟合目标映射 $\mathcal{H}(x)$,而是让它们拟合一个残差映射 $\mathcal{F}(x) = \mathcal{H}(x) - x$ 。
-
恒等映射(Shortcut Connections):通过“捷径连接”将输入 直接叠加到输出上,即最终输出为 $\mathcal{F}(x) + x$ 。
-
为什么有效:如果某一层保持恒等映射是最优的,那么将残差 $\mathcal{F}(x)$ 优化为 0,比用非线性层强行拟合一个恒等映射要容易得多 。
残差学习:一个构建模块
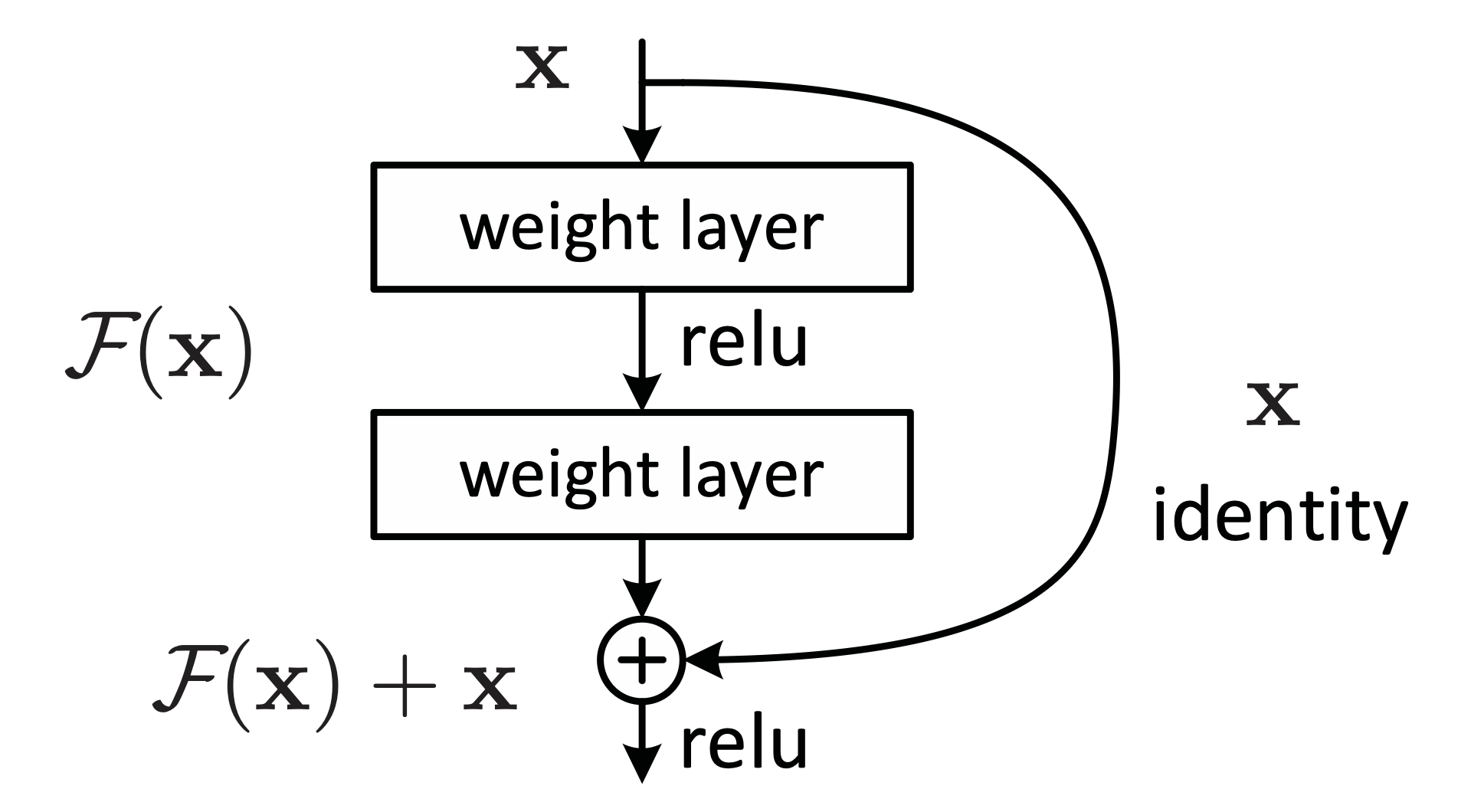
解决饱和与退化问题
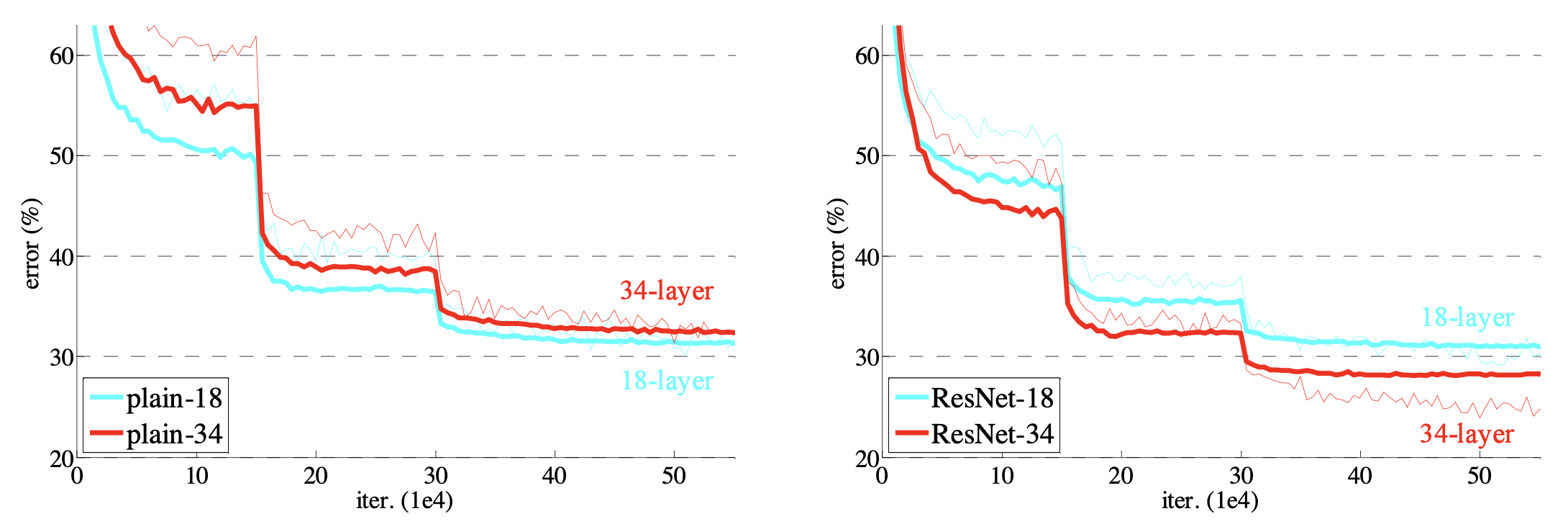
在 ImageNet 上训练。细曲线表示训练误差,粗曲线表示中心裁剪的验证误差。左图:18 层和 34 层的普通网络。右图:18 层和 34 层的 ResNet。在该图中,残差网络相对于对应的普通网络没有额外的参数。
降低计算复杂度的同时显著提升性能
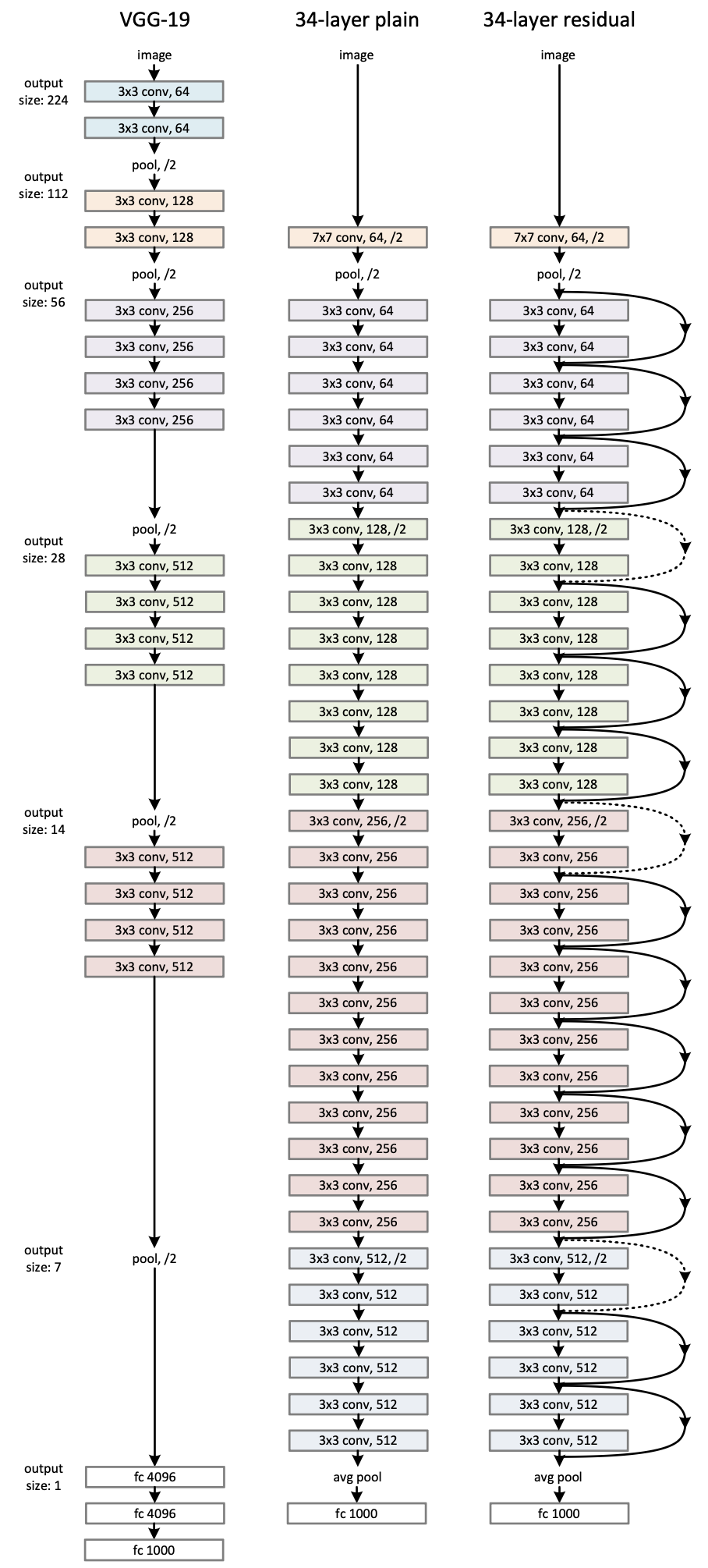
ImageNet 的示例网络架构。左图:作为参考的 VGG-19 模型 [41](196 亿 FLOPs)。中图:具有 34 个参数层的普通网络(36 亿 FLOPs)。右图:具有 34 个参数层的残差网络(36 亿 FLOPs)。虚线快捷连接用于增加维度。
超连接(Hyper-Connections, HC)
概述
超链接(Hyper-connections, HC) 是由字节跳动 Seed 基础模型团队(Seed-Foundation-Model Team)提出的一种新型网络连接方法,旨在作为深度神经网络中 残差连接(Residual Connections) 的有效替代方案 。实验的规模是 1B 和 7B 。
解决“跷跷板效应”:梯度消失与表征坍缩的平衡
在传统的残差连接中,两种主要的变体 Pre-Norm 和 Post-Norm 存在明显的权衡问题,被称为“跷跷板效应” :
-
Pre-Norm:虽然能有效缓解梯度消失问题,使深层网络更易训练,但容易导致表征坍缩(Representation Collapse)。即深层特征变得高度相似,增加层数带来的边际贡献减小 。
-
Post-Norm:可以缓解表征坍缩,但会重新引入梯度消失问题,使得训练非常深的网络变得困难 。 超链接通过允许网络自主学习连接强度,克服了这种权衡,同时保持了梯度的稳定性和表示的多样性 。
赋予网络自主学习连接强度的能力
残差连接预定义了层输入与输出之间的固定连接强度 。而超链接允许网络根据任务需求,自动调节不同深度特征之间的连接强度 。其核心思想包括:
-
可学习的深度连接(Depth-connections):可以看作是广义的残差连接,为每层的输入和输出分配权重 。
-
可学习的宽度连接(Width-connections):通过将网络输入扩展为 个副本(隐藏向量),允许同一层内的隐藏向量进行信息交换 。
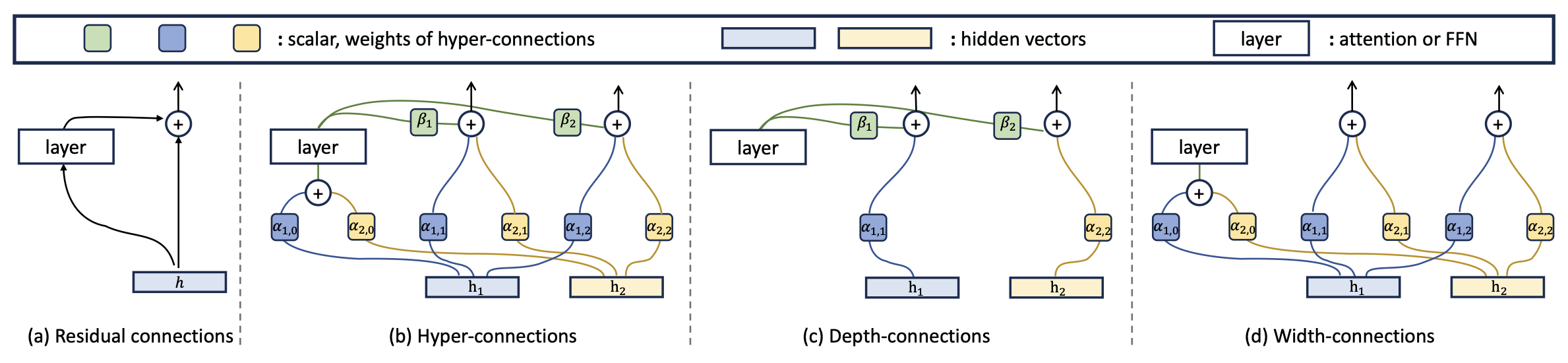
扩展倍数为 n=2 的超链接 (Hyper-connections, HC)。 (a) 残差连接 (Residual connections)。(b) 超链接 (Hyper-connections): 以及 $\beta_1, \beta_2, \alpha_{0,0}, \alpha_{0,1}, \alpha_{1,0}, \alpha_{1,1}, \alpha_{2,1}$ 是可学习的标量,或是由网络预测的标量(取决于具体的 HC 版本)。这些连接实现了特征在横向上的信息交换以及在深度方向上的纵向整合。它们可以被解耦为深度连接和宽度连接。(c) 深度连接 (Depth-connections):在层输出与隐藏向量 之间进行加权求和。(d) 宽度连接 (Width-connections):允许隐藏向量 与 之间进行信息交换。
静态超链接和动态超链接
-
静态超链接 (SHC):其连接权重矩阵 中的元素是可学习的标量参数 。这意味着在模型训练完成后,无论输入什么数据,层与层之间的连接强度(即权重)都是固定不变的 。
-
动态超链接 (DHC):其权重矩阵 是由网络根据当前输入实时预测的 。通过引入一个线性层和激活函数(如
tanh),网络能针对每一组输入数据动态调整连接权重 。
实验表明,DHC 的表现通常优于 SHC 。在大型语言模型(LLM)预训练中,DHC 的收敛速度显著快于基线模型,且在下游任务(如 ARC-Challenge)上提升更明显 。
SHC 提供了一种可学习但固定的架构优化,而 DHC 则赋予了模型一种随数据内容自适应调整内部信息流动的能力。
性能对比
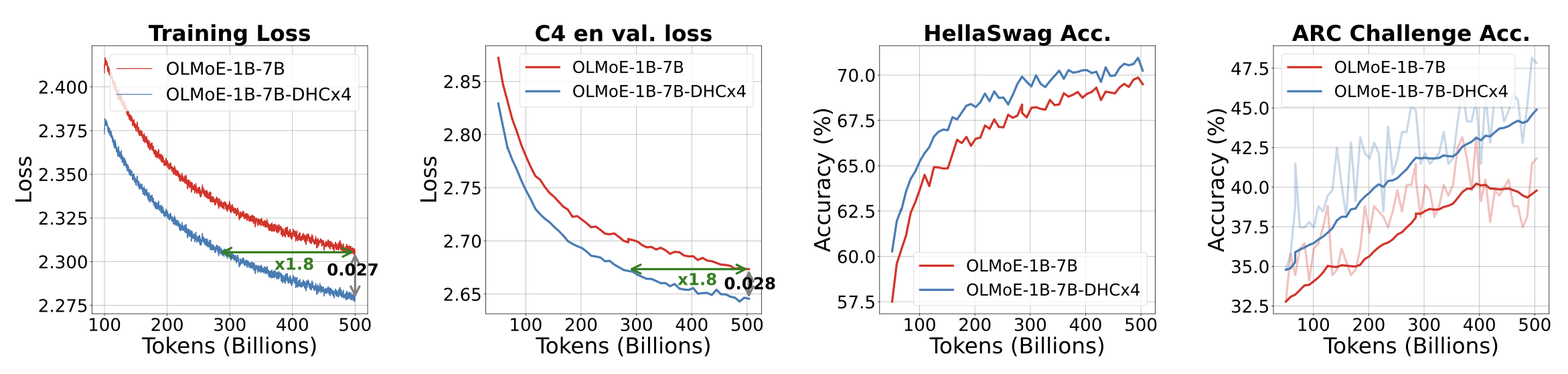
基准模型 OLMoE-1B-7B 与引入超连接(hyper-connections)的模型 OLMoE-1B-7B-DHC×4 的性能对比。(1)和(2)分别展示了训练损失(0.99 EMA 平滑后)和 C4-en 验证损失。相比基准模型收敛速度快 1.8 倍,并在 500B tokens 处保持显著优势。(3)和(4)展示了在 HellaSwag 和 ARC-Challenge 上的准确率曲线,证明了 OLMoE-1B-7B-DHC×4 模型的优越性能。
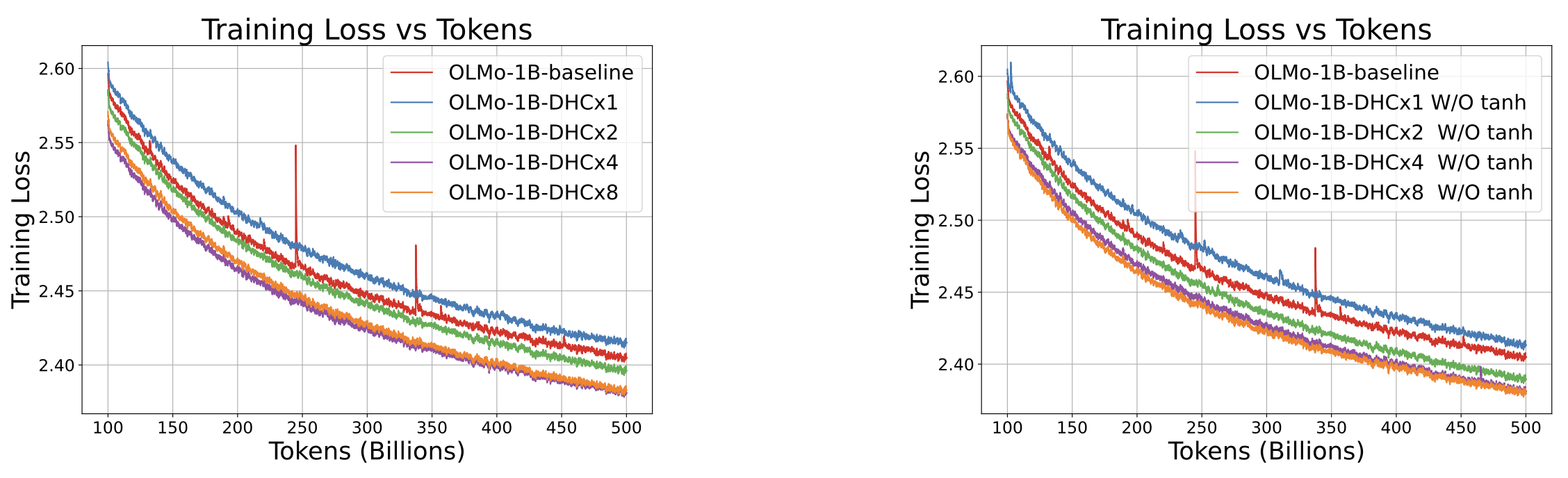
不同扩展倍率(Expansion Rate)下的训练损失曲线对比。 左侧子图展示了在不同扩展倍率下应用动态超链接(DHC)的模型表现;右侧子图则展示了省略 tanh 函数后的效果。两幅子图均表明,在 500B token 的训练过程中,提高扩展倍率能够显著提升训练损失性能。结果均采用系数为 0.99 的指数移动平均(EMA)进行了平滑处理。
深入分析:参数量(Parameters)、计算量(Computation)和内存占用(Memory Footprint)
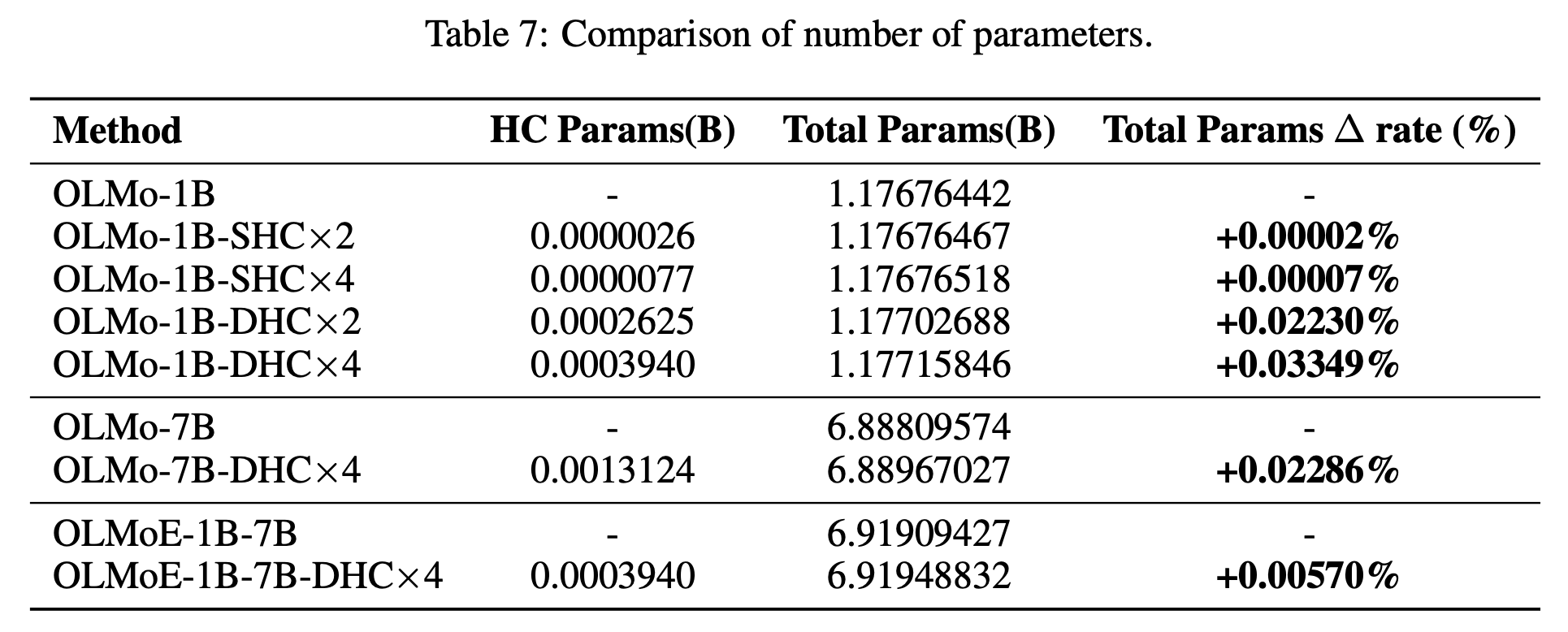
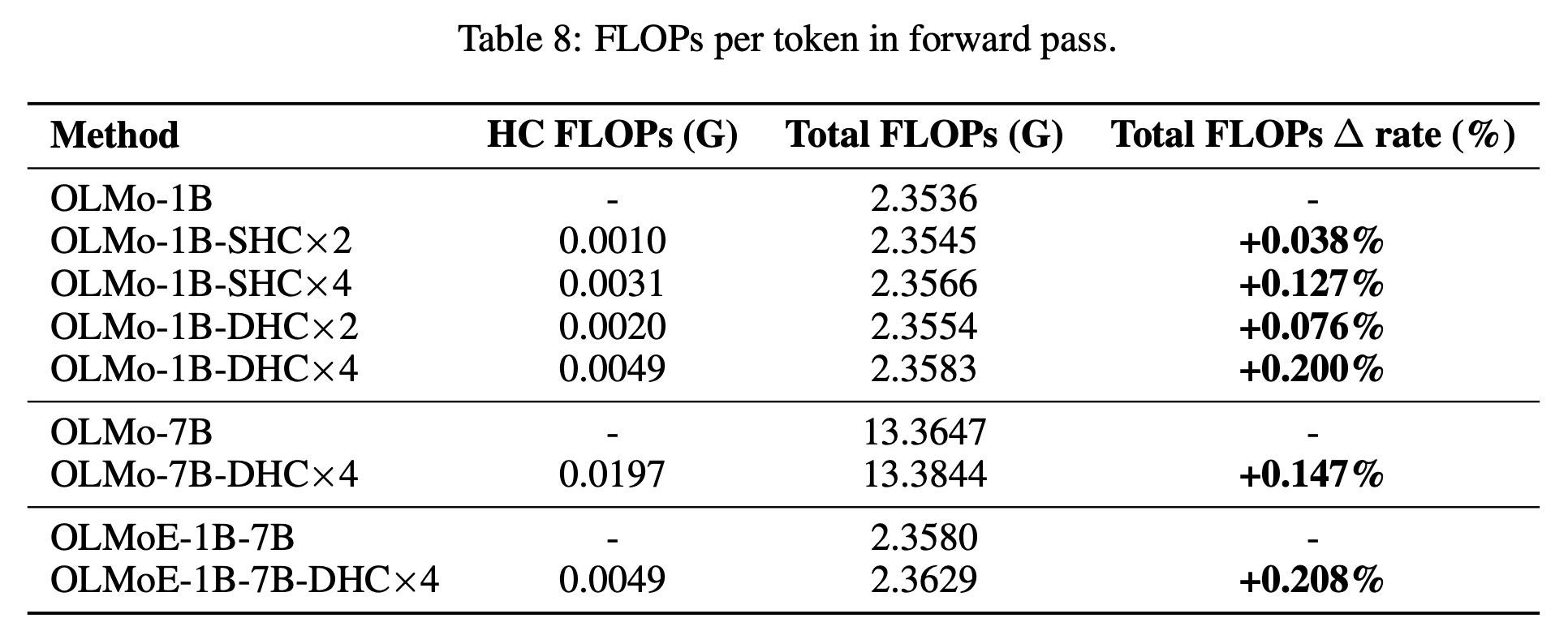
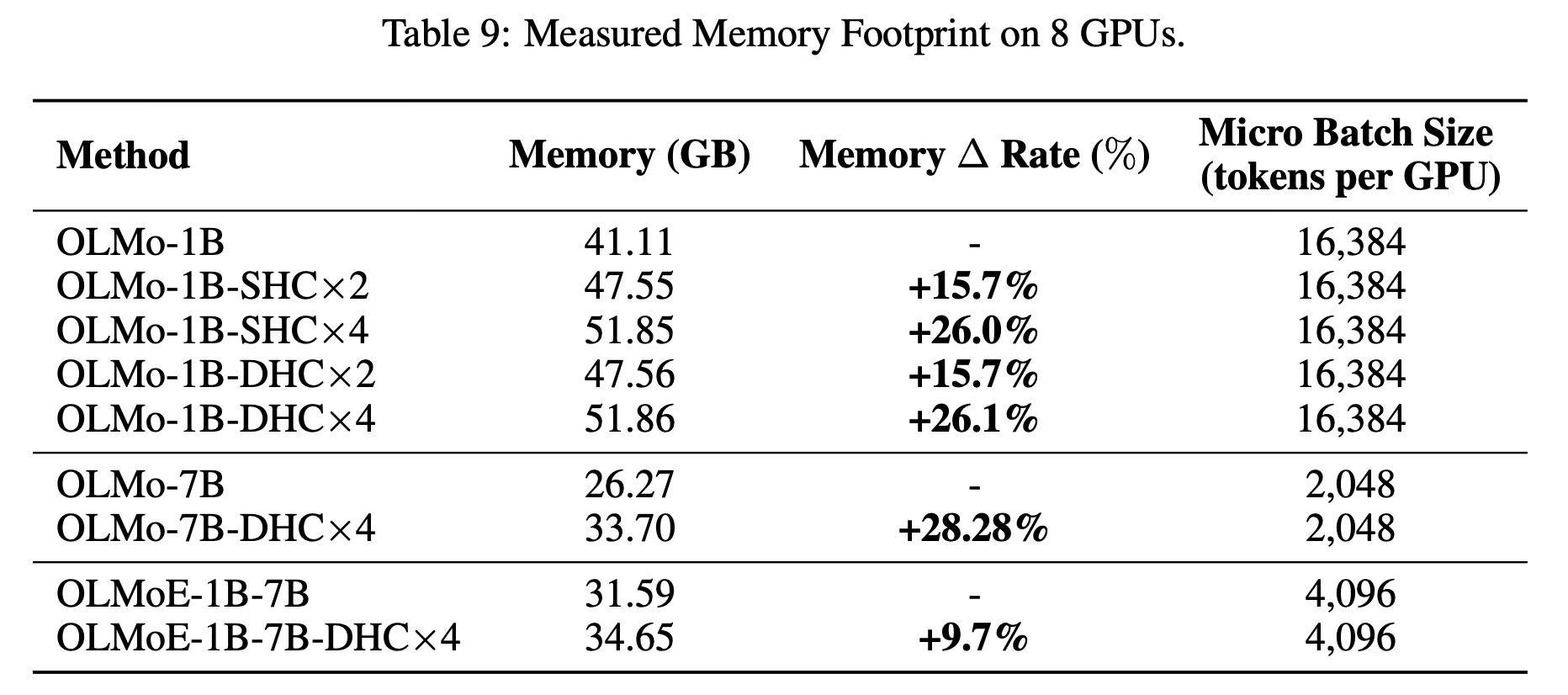
总结对比表
| 维度 | 残差连接 (Baseline) | 超链接 (HC) | 影响评估 |
|---|---|---|---|
| 参数量 | $P$ | $P + \text{tiny } \Delta$ | 几乎无感 |
| FLOPs (计算量) | $C$ | $C + \text{tiny } \Delta$ | 几乎无感 |
| 显存占用 | $M$ | $M \times (1 + \epsilon)$ | 略有增加,随 线性增长 |
| 训练收敛 | 标准 | 快 1.8 倍 | 显著效率提升 |
Transformer 中的超连接
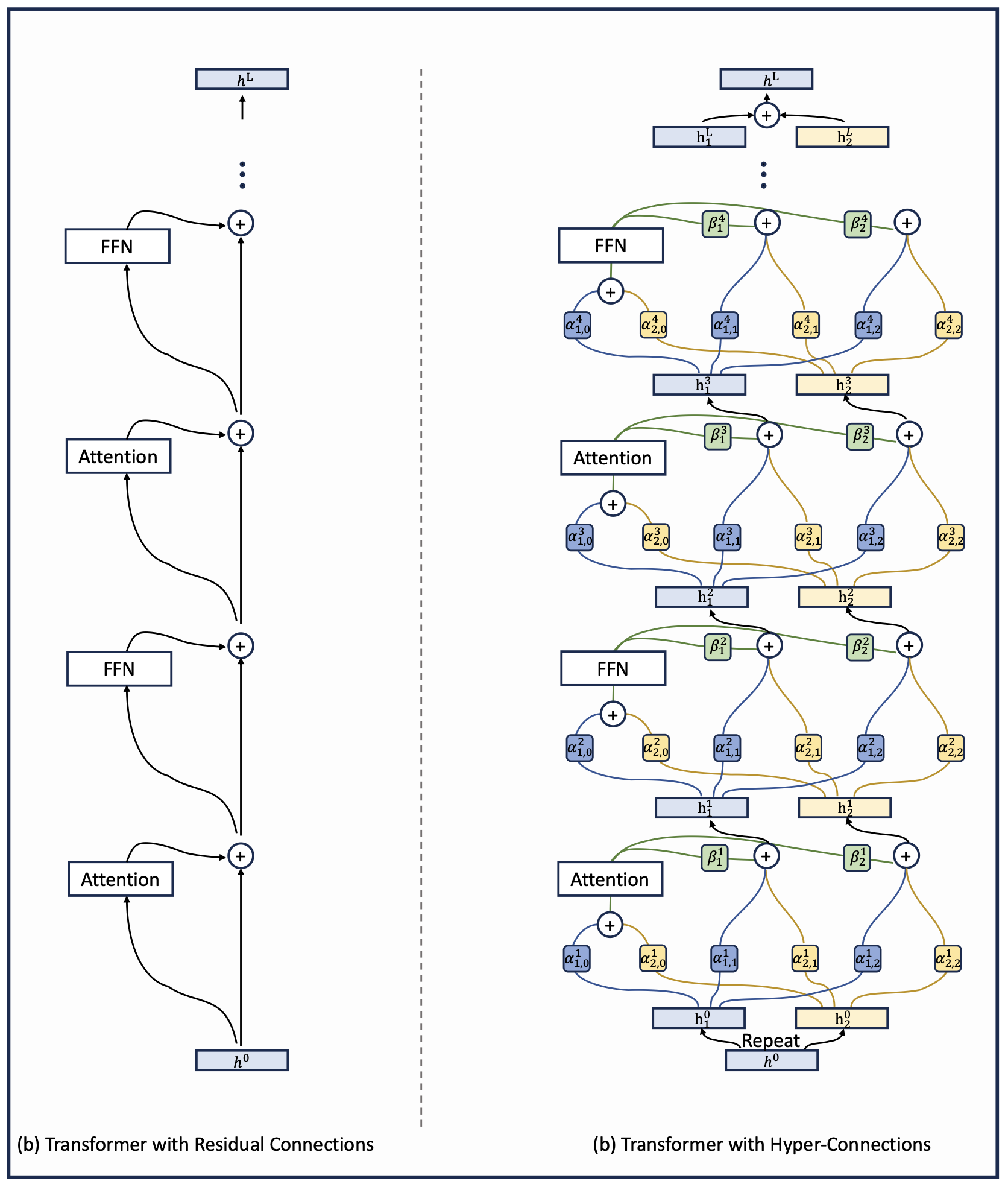
应用超链接(Hyper-connections)的 Transformer 与应用残差连接(Residual connections)的 Transformer 之间的对比。
流形约束超连接(Manifold-Constrained Hyper-Connections, mHC)
概述
mHC(Manifold-Constrained Hyper-Connections,流形约束超连接)是由 DeepSeek-AI 提出的一种新型神经网络架构框架 。它旨在改进原始的超连接(Hyper-Connections, HC),在保留其强大性能的同时,解决其在大规模训练中的不稳定和高效率开销问题 。实验的规模是 27B 。
核心背景:从残差连接到超连接
-
残差连接(Residual Connection):现代大模型(如 ResNet, Transformer)的基石,其核心是“恒等映射”(Identity Mapping),确保信号在深层网络中稳定传播 。
-
超连接(HC):通过拓宽残差流(将特征维度从 C 扩展到 n×C )并引入可学习的混合矩阵,增强了模型的拓扑复杂度和性能潜力 。
-
HC 的缺陷:由于混合矩阵是无约束学习的,模型在深度增加时会偏离恒等映射,导致信号无限放大或缩小(梯度爆炸/消失),在大规模训练(如 27B 参数量)中表现出极大的不稳定性 。
mHC 的核心原理:流形约束
mHC 的核心思想是将 HC 的连接空间投影到一个特定的流形上,以恢复恒等映射的特性 。
-
Birkhoff 多面体(Birkhoff Polytope):mHC 使用 Sinkhorn-Knopp 算法,将残差连接矩阵($\mathcal{H}_l^{res}$)投影为双随机矩阵(行和列之和均为 1 且元素非负) 。
-
稳定性保障:这种约束使得连接操作等同于特征的凸组合。由于双随机矩阵在矩阵乘法下具有封闭性,信号的均值和范数在跨层传播时能保持稳定,从而彻底解决了 HC 的数值不稳定性问题 。
基础设施优化(解决系统开销)
HC 虽然计算量(FLOPs)增加不多,但由于残差流变宽,带来了严重的显存和带宽瓶颈(“存储墙”问题) 。mHC 通过以下技术确保了训练效率:
-
算子融合(Kernel Fusion):将多个操作(如 RMSNorm 和矩阵乘法)合并为一个计算内核,减少内存带宽占用 。
-
选择性重算(Selective Recomputing):丢弃部分中间激活值并在反向传播时动态重算,大幅降低了显存占用 。
-
DualPipe 通信重叠:扩展了流水线并行调度,使 n (=4) 倍增加的通信开销能与计算更好地重叠,在大规模训练中仅引入约 6.7% 的额外耗时 。
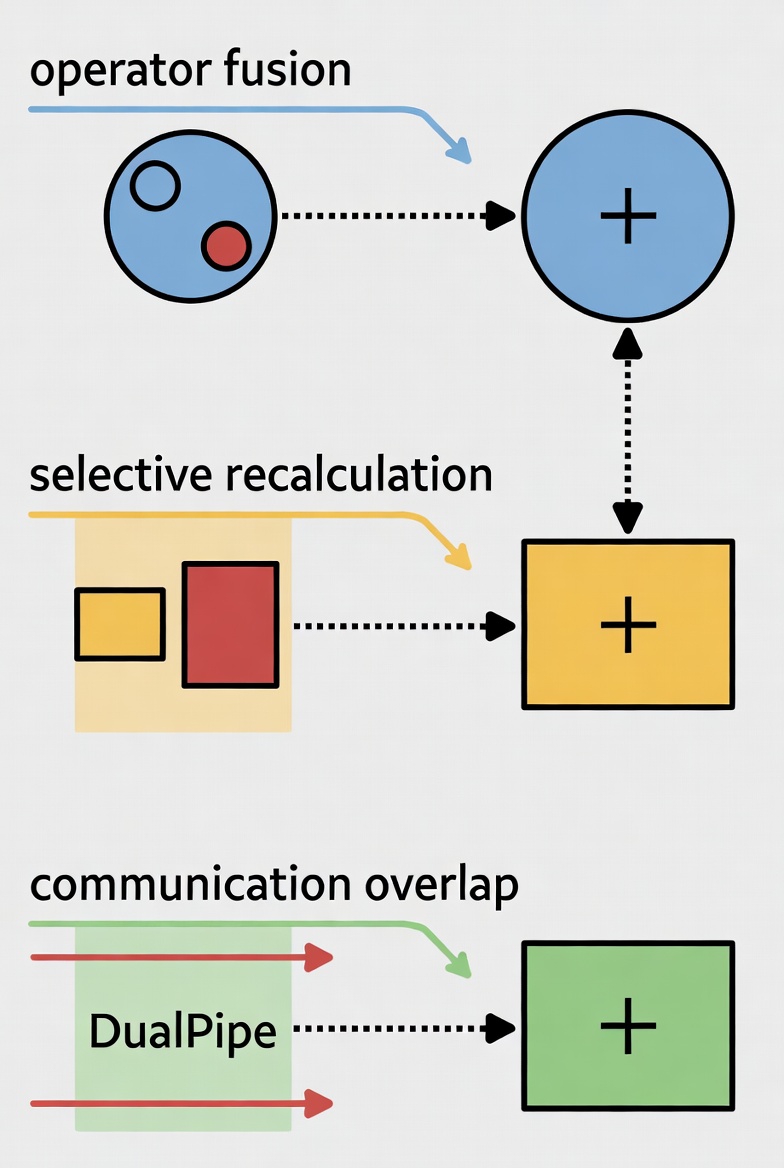
实验表现与意义
-
卓越的稳定性:在 27B 模型的实验中,mHC 成功消除了 HC 出现的损失函数激增和梯度异常现象 。
-
性能提升:在 BBH、GSM8K、MMLU 等多个主流 Benchmark 上,mHC 均显著优于传统的残差架构,且在大多数任务上优于原始 HC 。
-
可扩展性:证明了超连接架构可以稳定地扩展至极大规模的模型训练,为基础模型拓扑设计的演进提供了新方向 。
残差连接范式图解
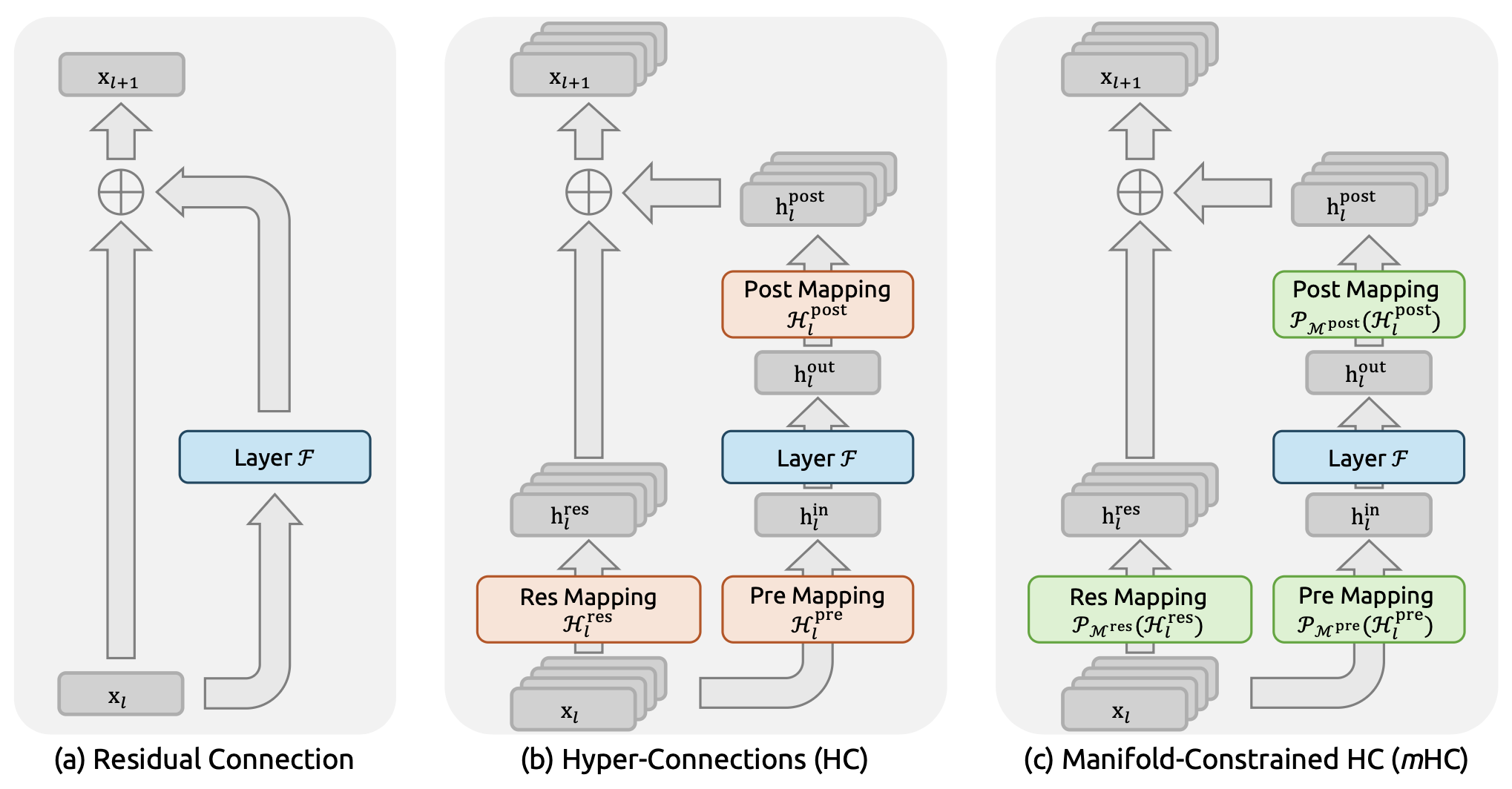
本图对比了以下三种结构设计:(a) 标准残差连接 (Residual Connection),(b) 超连接 (Hyper-Connections, HC),以及 (c) 流形约束超连接 (Manifold-Constrained Hyper-Connections, mHC)。与无约束的 HC 不同,mHC 致力于优化残差连接空间,通过将矩阵投影(Projecting matrices)到受限流形上,以确保训练的稳定性。
性能对比
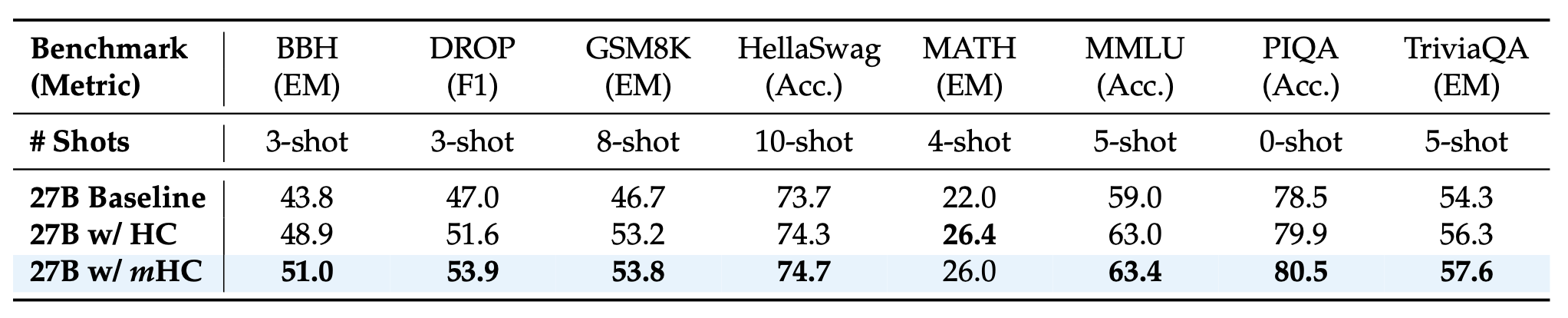
27B 规模模型的系统级基准测试结果。 本表对比了基线模型(Baseline)、超链接模型(HC)以及流形约束超链接模型(mHC)在 8 个不同下游基准测试中的零样本(zero-shot)和少样本(few-shot)性能。mHC 一致性地优于基线模型,并在大多数基准测试中超越了 HC,证明了其在大规模预训练中的有效性。
27B w/HC 相比 27B Baseline 的提升
| 基准测试 | Baseline | w/HC | 提升幅度 (%) |
|---|---|---|---|
| BBH | 43.8 | 48.9 | +11.64% |
| DROP | 47.0 | 51.6 | +9.79% |
| GSM8K | 46.7 | 53.2 | +13.92% |
| HellaSwag | 73.7 | 74.3 | +0.81% |
| MATH | 22.0 | 26.4 | +20.00% |
| MMLU | 59.0 | 63.0 | +6.78% |
| PIQA | 78.5 | 79.9 | +1.78% |
| TriviaQA | 54.3 | 56.3 | +3.68% |
- 平均提升:约 8.55%
27B w/mHC 相对于 27B w/HC 的性能提升
计算公式:
| 基准测试 | 27B w/HC | 27B w/mHC | 提升幅度 (%) |
|---|---|---|---|
| BBH | 48.9 | 51.0 | +4.29% |
| DROP | 51.6 | 53.9 | +4.46% |
| GSM8K | 53.2 | 53.8 | +1.13% |
| HellaSwag | 74.3 | 74.7 | +0.54% |
| MATH | 26.4 | 26.0 | -1.52% |
| MMLU | 63.0 | 63.4 | +0.63% |
| PIQA | 79.9 | 80.5 | +0.75% |
| TriviaQA | 56.3 | 57.6 | +2.31% |
- 平均提升:约 1.57%
扩展实验(Scaling Law)
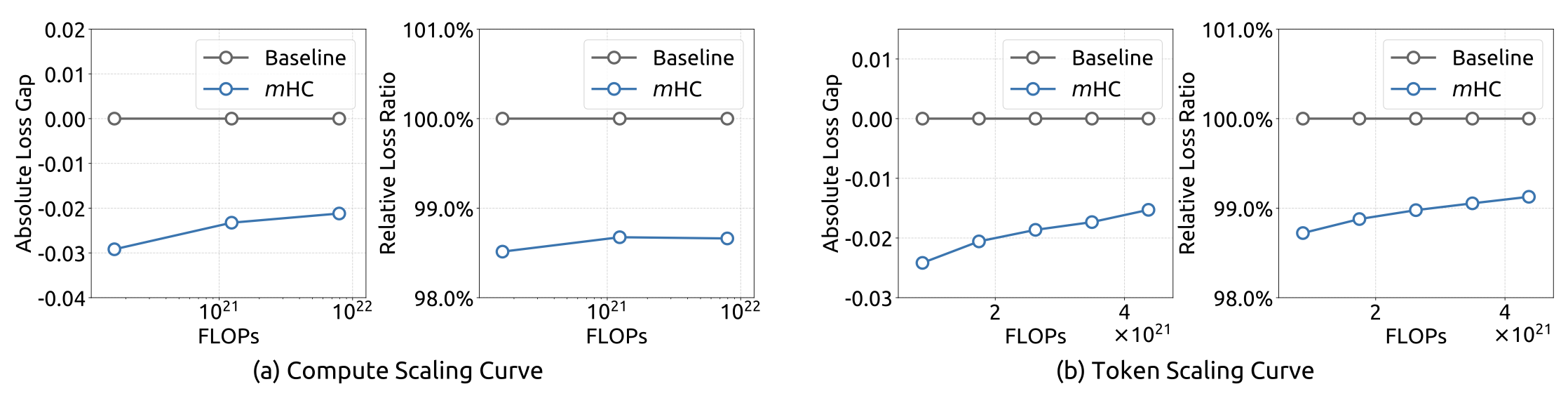
mHC 与基线模型(Baseline)的扩展特性(Scaling properties)对比。 (a) 计算扩展曲线:实线描绘了在不同计算预算下的性能差距。每个点代表了模型规模与数据集规模的特定计算最优配置,涵盖了从 3B、9B 到 27B 参数的扩展。 (b) Token 扩展曲线:3B 模型在训练过程中的轨迹。每个点代表模型在不同训练 token 量下的性能表现。